Inhaltsverzeichnis
GNU Octave
GNU Octave ist ein freies Programm für numerisches Rechnen.
Plotting
GNU Octave hat zwei typische Grafik-Toolkits; fltk und GNUplot.
Um zu sehen welches aktiv ist kann einfach
graphics_toolkit
eingegeben werden.
Um das Toolkit zu wechseln kann einfach
graphics_toolkit("gnuplot")
eingegeben werden.
2D-Plots
Um einen 2D-Plot zu machen kann die Funktion plot() verwendet werden.
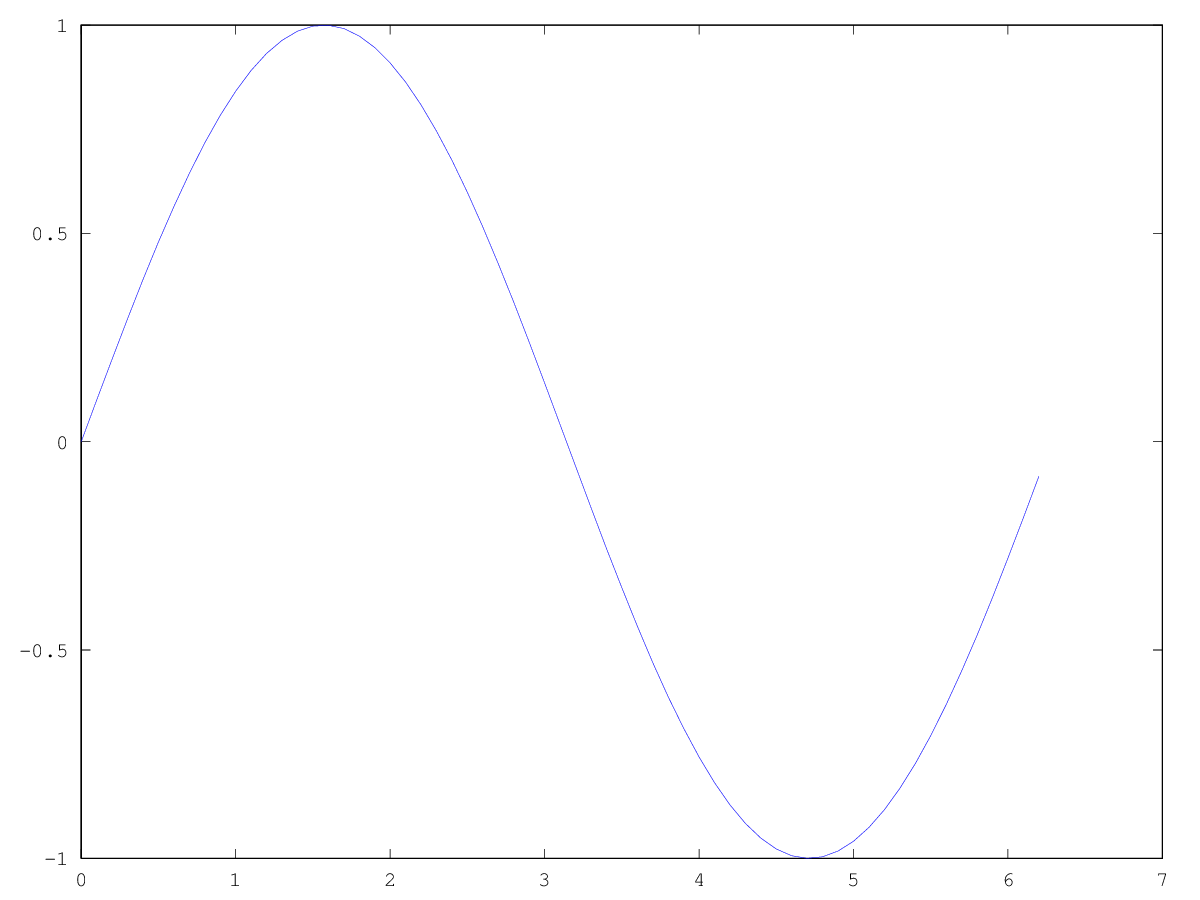
x = [0:0.1:2*pi]; a = sin(x); plot(x,a)
erzeugt
Um mehrere Kurven übereinander zu legen kann hold on und hold off verwendet werden.
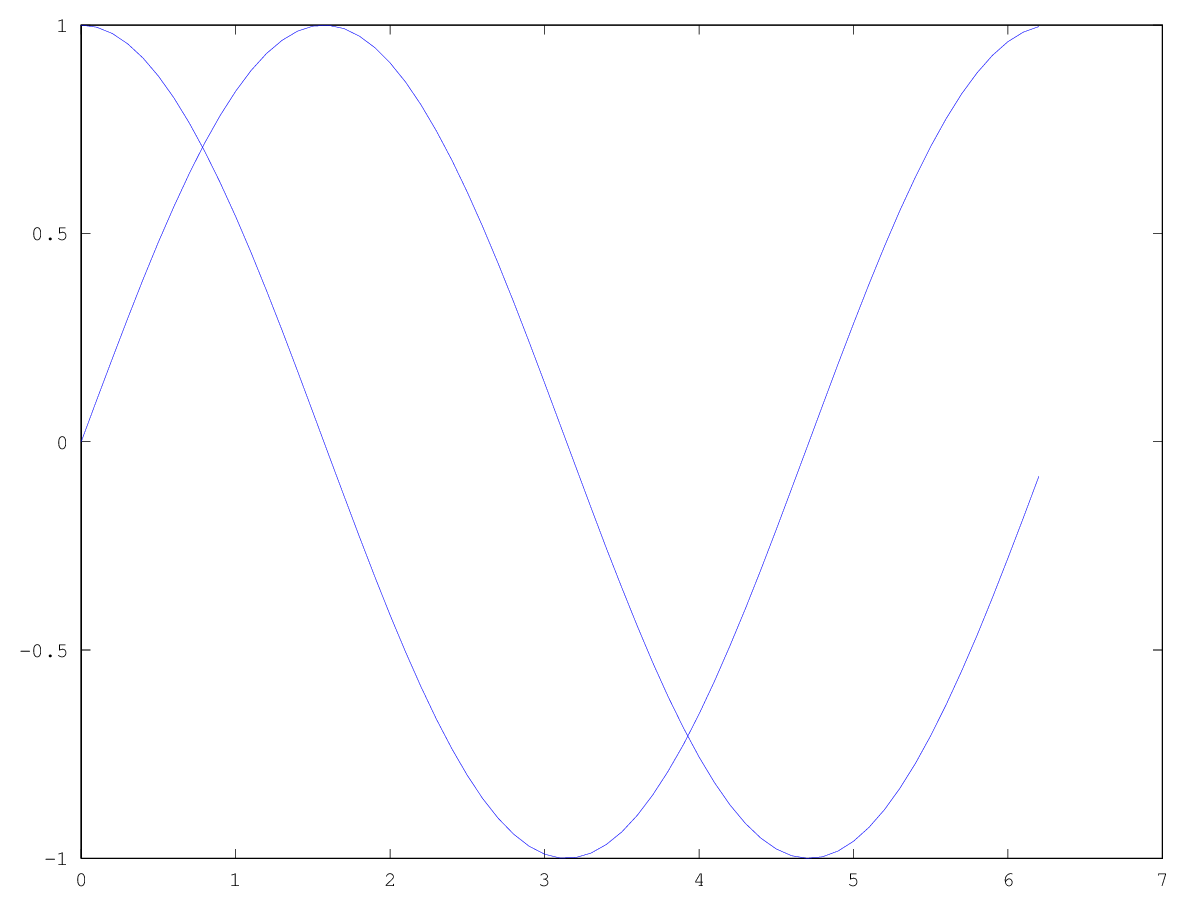
x = x = [0:0.1:2*pi]; a = sin(x); b = cos(x); hold on plot(x,a) plot(x,b) hold off
erzeugt
3D-Plots
Um einen 3D-Plot zu erzeugen kann die Funktion plot3() benutzt werden.
x = [0:0.001:2*pi]; a = sin(x); b = cos(x); plot3(x,a,b);
Für fancy Plots kann man aber auch mesh() benutzen.
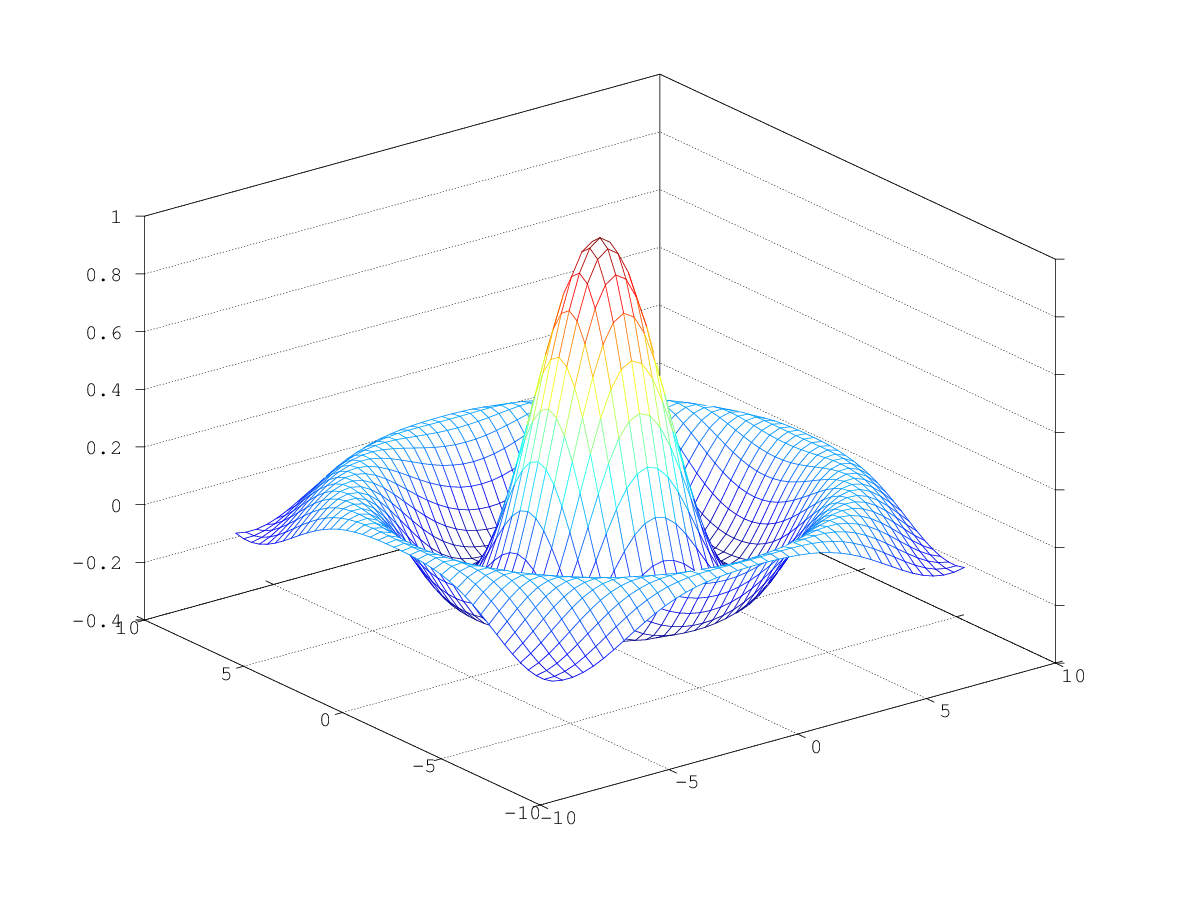
tx = ty = linspace (-8, 8, 41)'; [xx, yy] = meshgrid (tx, ty); r = sqrt (xx .^ 2 + yy .^ 2) + eps; tz = sin (r) ./ r; mesh (tx, ty, tz);
erzeugt
Packages
GNU Octave hat ein eigenes Package-System. Mit diesem können neue Packages installiert und geladen werden.
Package installieren
Um ein Package zu installieren kann es entweder manuell heruntergeladen werden etc. oder man greift direkt mit dem Package-Manager von Octave auf die offiziellen Packages von Octave-Forge zu.
pkg install -forge package_name
Package laden
pkg load package_name
Empfehlenswerte Packages
Liste offizieller Packages
Regelungstechnik
Control Package installieren
pkg install -forge control
Package laden
pkg load control
s definieren als Variable des Laplace-Bereichs
s = tf('s')
erzeugt
Transfer function 's' from input 'u1' to output ... y1: s Continuous-time model.
Übertragungsfunktion definieren
G = 1/(1+s)
erzeugt
Transfer function 'G' from input 'u1' to output ...
1
y1: -----
s + 1
Continuous-time model.
Bode-Plot erstellen (Amplituden- & Phasegang)
bode(G)
erzeugt
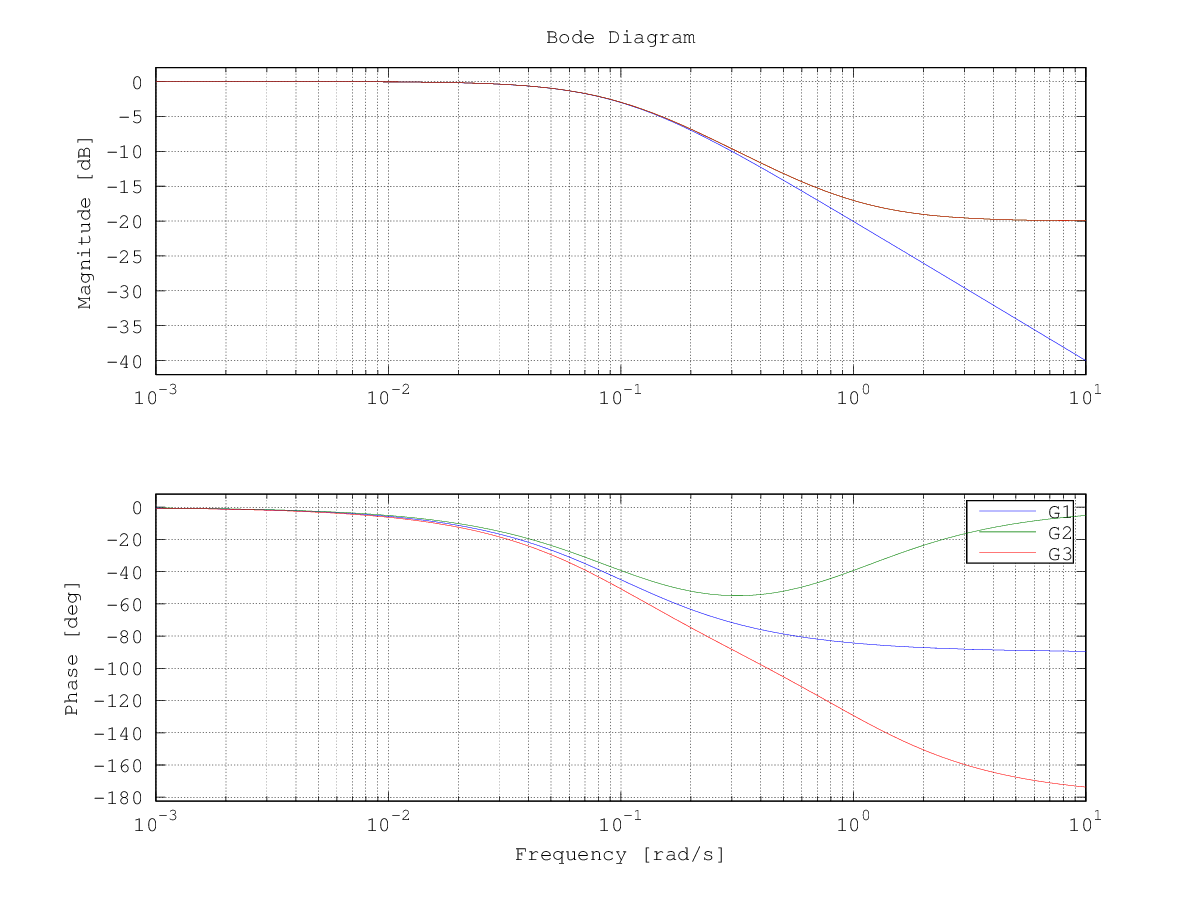
Es können aber auch mehrere Kurven zusammen geplottet werden.
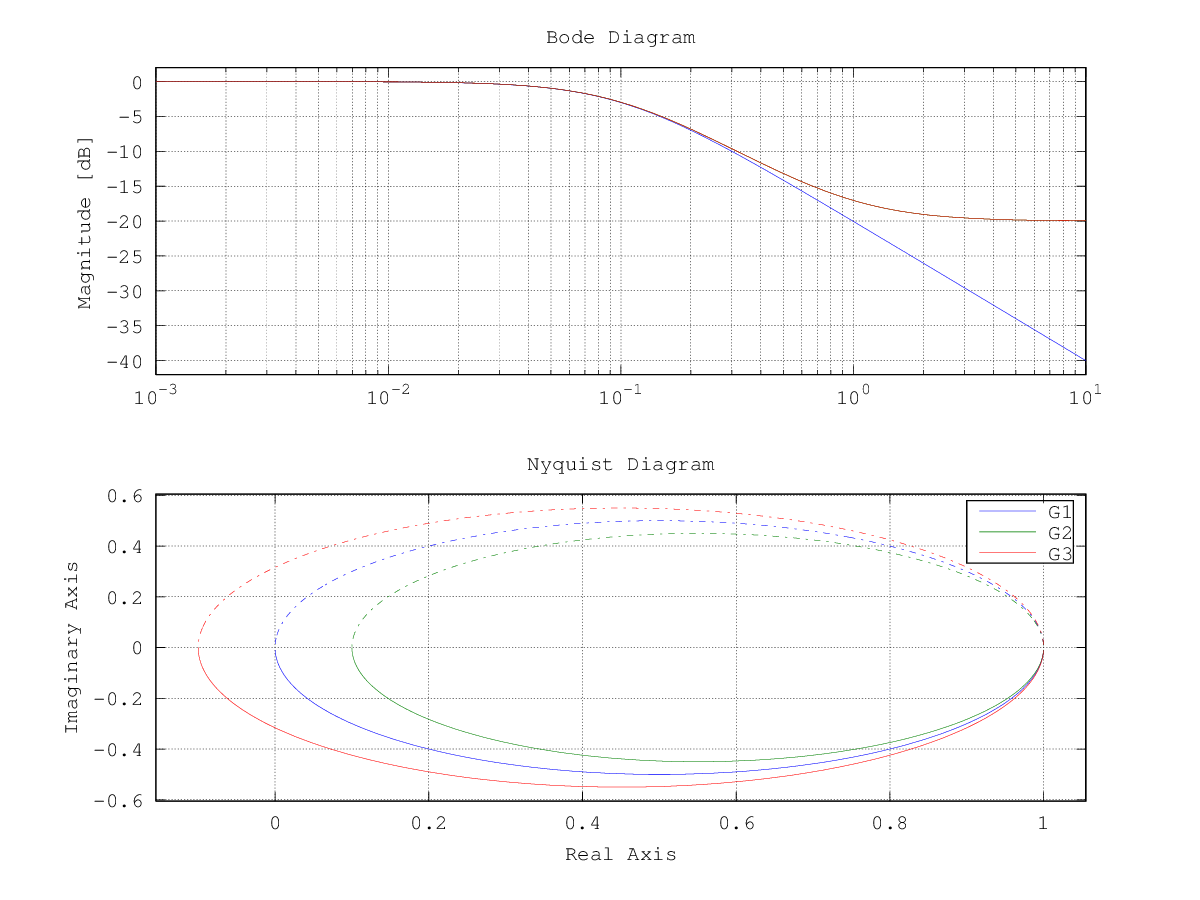
G1 = 1/(1+10*s) G2 = (1+s)/(1+10*s) G3 = (1-s)/(1+10*s) bode(G1,G2,G3)
erzeugt
Nyquist-Plot erstellen
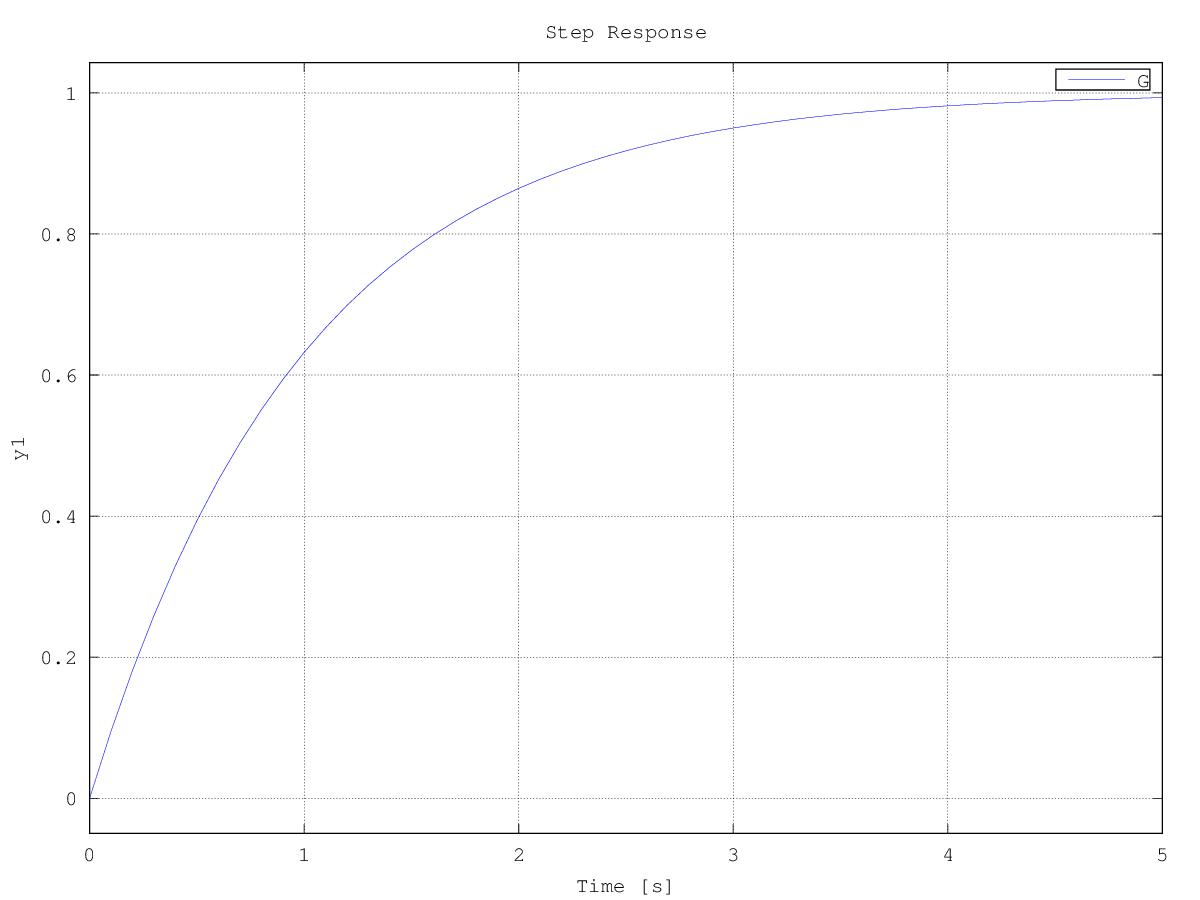
Sprungantwort
Plot exportieren/speichern
GNU Octave hat verschiedene Toolkits für Grafiken. Diese bieten jeweils verschiedene Möglichkeiten fürs exportieren. Die folgenden Beispiele behandeln das Toolkit GNUPlot.
print -dsvg myplot.svg
Diskrete Transferfunktionen
Um diskrete Transferfunktionen zu behandeln, kann ein solches System ähnlich wie ein kontinuierliches System definiert werden, wobei noch ein Parameter folgt für das Abtastintervall (Sampling Time). Der Wert für das Abtastintervall verändert nur die Skalierungen beim Bode-Plot etc. nicht aber deren Verlauf.
N = [1 1 1]; % numerator polynomial D = [1 1]; % denumerator polynomial Ts = 1; % sampling time H = tf([1 1 1], [1 1], Ts);
Der obige Code ergibt die Ausgabe
Transfer function 'H' from input 'u1' to output ...
z^2 + z + 1
y1: -----------
z + 1
Sampling time: 1 s
Discrete-time model.
Umwandlung kontinuierliche in zeitdiskrete Transferfunktion
Oft ist es einfacher das Problem im Zeitkontinuerlichen zu lösen und danach einfach ins Zeitdiskrete umzuformen. Dies kann mittels unterschiedlicher Methoden erfolgen. Die bekanntesten Transformationen sind die ZOH (Zero Order Hold) und bilinieare (Tustin) Transformation.
Die Transformation kann in Octave mittels der Funktion c2d() durchgeführt werden.
N = [1 1]; % numerator polynomial D = [1 1 1]; % denumerator polynomial Ts = 1; % sampling time G_tcont = tf(N, D); % time-continuous transfer function G_tdisc = c2d(G_tcont, Ts); % time-discrete transfer funtion
Transfer function 'G_tdisc' from input 'u1' to output ...
0.8738 z - 0.2918
y1: -----------------------
z^2 - 0.7859 z + 0.3679
Sampling time: 1 s
Discrete-time model.
Wichtig ist, daran zu denken, dass die beiden Transferfunktionen nicht identisch sind. Dies lässt sich mit einem Bode-Diagramm deutlich machen. Die Transformation führt insbesondere zu Phasenverlusten je höher die Sampling-Zeit ist (je höher die Frequenz, desto weniger Abweichung).